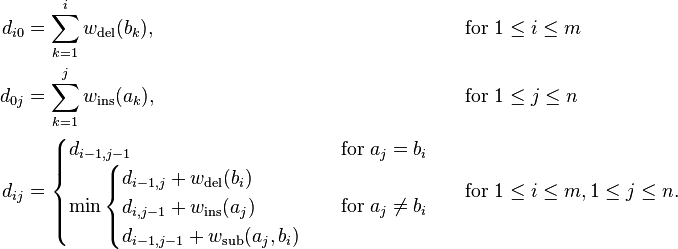Write a program to solve a Sudoku puzzle by filling the empty cells.
Empty cells are indicated by the character '.'.
You may assume that there will be only one unique solution.


A sudoku puzzle... ...and its solution numbers marked in red.
Hide Tags
Backtracking Hash Table
Hide Similar Problems
(E) Valid Sudoku
本来以为是拼脑力的一道题,没想到拼的只是体力,无趣程度仅次于罗马字数字互转那两道题。
拿到题目首先想到的自然是回溯,
同时还想到的是,对每个空位,最好是能基于行,列,所在九宫列出可用的数字,这样便于减少循环嘛。
所以写了一个基于这个思路的 solution,在每个空格都计算available的数字,并从中选择然后递归。
递归的时候被一个破问题 block 了不少时间:
起初的做法是,先 [x][y+1] 递归进去,做完返回之后再 [x+1][y] 递归,就是这里坏事了。
从 [0][0] 开始,一路横着递归到 [0][8],然后因为此时 y<8 不成立,所以一路纵向递归到 [8][8],然后逐步返回。
返回到 [0][8],此格的递归全部完成,因此再次返回,来到 [0][7],
在 [0][7] 这里,是从 [x][y+1] 返回的,所以还需要做 [x+1][y],于是进入第二部分递归,一路纵向直到 [7][8]。
问题就在这里,一旦在到 [7][8] 的途中出现 false,就会往回退,
但是!退到 [0][7] 之后,再回退是回退到 [0][6],而不是已经填过数字的第 8 列!!
这就意味着,回退清除已经填充的数字的时候,右边已经填充的列们,是不会被清除的。。。!!
换句话说,回溯回不去了!!
在这里郁闷了好一阵子,四个方向 dfs 也不对,怎么才能回去呢?想来想去没有好的法子。
最后参考了网上的帖子里的做法,一行走到最右边,强制再从下一行的最左边开始……
是的,改成这样之后,问题解决了,除去下标运算没有减去 ‘1’ 的问题,计算出了正确答案,耗时 56 ms,不算好。
但是怎么看怎么觉得别扭,丑陋如斯!
class Solution {
public:
//----------------------- calculate availabe numbers then recursive -----------------------
void solveSudoku_dave(vector<vector<char>>& board) {
if(9==board.size() && 9==board[0].size())
{
vector<vector<bool>> tried(9, vector<bool>(9));
fill(board, 0, 0, tried);
}
}
bool fill(vector<vector<char>>& board, int x, int y, vector<vector<bool>>& tried)
{
bool rst = true;
if(9>x && 9>y)
{
vector<char> ava;
char cc = board[x][y];
if('.' == cc)
{
available(board, x, y, ava);
if(!ava.size())
return false;
}
else
ava.push_back(cc);
for(auto a : ava)
{
tried[x][y] = true;
board[x][y] = a;
rst = true;
if(rst && y<8 && false==tried[x][y+1])
rst &= fill(board, x, y+1, tried);
if(8==y)
rst &= fill(board, x+1, 0, tried);
//就是在这里给自己挖了个坑,并且只能用丑陋无比的回0来解决。
//if(rst && x<8 && false==tried[x+1][y])
// rst &= fill(board, x+1, y, tried); if(false == rst)
board[x][y] = cc, tried[x][y]=false;
else
break;
}
}
return rst;
}
void available(vector<vector<char>>& board, int x, int y, vector<char>& ava)
{
int num[]={1,2,3,4,5,6,7,8,9};
for(int ii=0; ii<9; ++ii)
{
int idx = board[x][ii]-'1', idy=board[ii][y]-'1';
if('.' != board[x][ii])
num[idx] = -1;
if('.' != board[ii][y])
num[idy] = -1;
}
int blk_xstart=(x)/3*3, blk_ystart=(y)/3*3, blk_xend=blk_xstart+3, blk_yend=blk_ystart+3;
for(int ii=blk_xstart; ii<blk_xend; ++ii)
{
for(int jj=blk_ystart; jj<blk_yend; ++jj)
{
int idx = board[ii][jj]-'1';
if(0<num[idx] && '.' != board[ii][jj])
num[idx] = -1;
}
}
for(int ii=0; ii<9; ++ii)
if(0<num[ii])
ava.push_back((char)(num[ii]+'0'));
}
};
56 ms.
网上的帖子里流行的做法,大多数是不管三七二十一,对空的格子直接 1 到 9 循环尝试,
每次填入一个值,在借鉴Valid Sudoku的思路,判定整个矩阵是否合乎规则,
有效的话,就递归去搞定下一个空格,不行就回头再重来,直到最后。
整个操作的过程,是在 for 循环里做的,应该不算是 DFS ,但倒可以算是“回溯”。。。
隐约觉得这个应该更加费时,参照一个帖子写了一个,果不其然,80 ms,
参照另一个帖子做了一点优化,每次递归不要从头开始查,而是接着已经走过的部分继续查,
有些提高,从 80 ms 到了 64 ms,没有更好了。
class Solution {
public:
//-------------------- no available calculation, do 1~9 each time --------------------
void solveSudoku2(vector<vector<char>>& board) {
if(9==board.size() && 9==board[0].size())
solving(board, 0, 0);
}
//没有优化,每次重头查
bool solving(vector<vector<char>>& board)
{
for(int ii=0; ii<9; ++ii)
{
for(int jj=0; jj<9; ++jj)
{
if('.'==board[ii][jj])
{
for(char cc='1'; cc<='9'; ++cc)
{
board[ii][jj] = cc; //try all possible values
if(isValid(board, ii, jj)
&& solving(board)) //recursive call, backtracking
return true;
board[ii][jj] = '.'; //recover old value when go back
}
return false; //all possible numbers are tried.
}
}
}
return true; //no more '.' to solve
}
//优化之后,从现有位置继续
bool solving(vector<vector<char>>& board, int xx, int yy)
{
for(int ii=xx; ii<9; ++ii)
{
for(int jj=(0+(xx==ii)?yy:0); jj<9; ++jj) //jj=yy, then =0 !!
{
if('.'==board[ii][jj])
{
for(char cc='1'; cc<='9'; ++cc)
{
board[ii][jj] = cc; //try all possible values
if(isValid(board, ii, jj)
//recursive call from next element, backtracking
&& solving(board, ii+(8==jj), (8==jj)?0:(jj+1)))
return true;
board[ii][jj] = '.'; //recover old value when go back
}
return false; //all possible numbers are tried.
}
}
}
return true; //no more '.' to solve
}
bool isValid(vector<vector<char>>& board, int x, int y)
{
for(int ii=0; ii<9; ++ii)
if((y!=ii && board[x][ii]==board[x][y]) || (x!=ii && board[ii][y]==board[x][y]))
return false;
int blk_xstart=(x)/3*3, blk_ystart=(y)/3*3, blk_xend=blk_xstart+3, blk_yend=blk_ystart+3;
for(int ii=blk_xstart; ii<blk_xend; ++ii)
for(int jj=blk_ystart; jj<blk_yend; ++jj)
if(ii!=x && jj!=y && board[ii][jj]==board[x][y])
return false;
return true;
}
};
64 ms.
看看性能有减无增,就跑去讨论区里看,本来以为会有什么精巧的算法,结果…,大失所望。
基本上一句话,空间换时间。
例如下面这个例子,弄三个全矩阵的 buffer,本别标记行/列/所在九宫的占用情况,占用即更新。
号称是 dfs,实际上看看那个 while,完全等于两重 for 循环,这也能叫 dfs…
另外那句“ board[row][col] = '.'; ”,原文是在 1~9 的 for 循环之后,功能上没问题,因为只判断 buffer么,
但是语义上不能算对,应该挪到 for 循环里头。
class Solution {
public:
//----------------------------- full buffer for quick check -----------------------------
void buildUsedFlag(vector<vector<char>> &board,
bool rowUsed[9][9], bool colUsed[9][9], bool blkUsed[9][9])
{
for(auto i=0; i<9 ; ++i)
for(auto j=0; j<9; ++j)
if(board[i][j]!='.')
rowUsed[i][board[i][j]-'1'] = true,
colUsed[j][board[i][j]-'1'] = true,
blkUsed[(i/3) *3 +(j/3)][board[i][j]-'1'] =true ;
}
bool dfs(vector<vector<char>> &board, int row, int col,
bool rowUsed[9][9], bool colUsed[9][9], bool blkUsed[9][9])
{
while(row < 9 && board[row][col] != '.')
{
row += (col+1)/9;
col = (col+1) % 9;
}
if(row==9)
return true;
int i, blkIdx = (row/3) * 3 + col/3;
for(i=0; i<9; i++)
{
if(rowUsed[row][i] || colUsed[col][i] || blkUsed[blkIdx][i])
continue;
rowUsed[row][i] = colUsed[col][i] = blkUsed[blkIdx][i] = true;
board[row][col] = '1' + i;
if(dfs(board, row, col, rowUsed, colUsed, blkUsed))
return true;
board[row][col] = '.';
rowUsed[row][i] = colUsed[col][i] = blkUsed[blkIdx][i] = false;
}
return false;
}
void solveSudoku(vector<vector<char>>& board) {
bool rowUsed[9][9], colUsed[9][9], blkUsed[9][9];
fill_n(&rowUsed[0][0], 81, false);
fill_n(&colUsed[0][0], 81, false);
fill_n(&blkUsed[0][0], 81, false);
buildUsedFlag(board, rowUsed, colUsed, blkUsed);
dfs(board, 0, 0, rowUsed, colUsed, blkUsed);
}
};
4 ms.
后来看到一个算是有点意思的解法:
其实也还算是空间换时间,但同时也通过限制条件来提前算好了每个空的格子的可能取值,
而且这个限制条件的矩阵是随着每次填入的值来动态更新的,这个挺有创意。(这一部分可以借鉴到自己的代码里)
另外就是对于每个元素的可能性进行排序,从而尽可能减少不必要的反复尝试,犀利。(这个真没想到)
class Solution {
struct cell // encapsulates a single cell on a Sudoku board
{
uint8_t value; // cell value 1..9 or 0 if unset
// number of possible (unconstrained) values for the cell
uint8_t numPossibilities;
// if bitset[v] is 1 then value can't be v
bitset<10> constraints;
cell() : value(0), numPossibilities(9),constraints() {};
};
array<array<cell,9>,9> cells;
// sets the value of the cell to [v]
// the function also propagates constraints to other cells and deduce new values where possible
bool set(int i, int j, int v)
{
// updating state of the cell
cell& c = cells[i][j];
if (c.value == v)
return true;
if (c.constraints[v])
return false;
c.constraints = bitset<10>(0x3FE); // all 1s
c.constraints.reset(v);
c.numPossibilities = 1;
c.value = v;
// propagating constraints
for (int k = 0; k<9; k++) {
// to the row:
if (i != k && !updateConstraints(k, j, v))
return false;
// to the column:
if (j != k && !updateConstraints(i, k, v))
return false;
// to the 3x3 square:
int ix = (i / 3) * 3 + k / 3;
int jx = (j / 3) * 3 + k % 3;
if (ix != i && jx != j && !updateConstraints(ix, jx, v))
return false;
}
return true;
}
// update constraints of the cell i,j by excluding possibility of 'excludedValue'
// once there's one possibility left the function recurses back into set()
bool updateConstraints(int i, int j, int excludedValue)
{
cell& c = cells[i][j];
if (c.constraints[excludedValue]) {
return true;
}
if (c.value == excludedValue) {
return false;
}
c.constraints.set(excludedValue);
if (--c.numPossibilities > 1)
return true;
for (int v = 1; v <= 9; v++) {
if (!c.constraints[v]) {
return set(i, j, v);
}
}
assert(false);
}
// backtracking state - list of empty cells
vector<pair<int, int>> bt;
// find values for empty cells
bool findValuesForEmptyCells()
{
// collecting all empty cells
bt.clear();
for (int i = 0; i < 9; i++) {
for (int j = 0; j < 9; j++) {
if (!cells[i][j].value)
bt.push_back(make_pair(i, j));
}
}
// making backtracking efficient by pre-sorting empty cells by numPossibilities
sort(bt.begin(), bt.end(), [this](const pair<int, int>&a, const pair<int, int>&b) {
return cells[a.first][a.second].numPossibilities < cells[b.first][b.second].numPossibilities; });
return backtrack(0);
}
// Finds value for all empty cells with index >=k
bool backtrack(int k)
{
if (k >= bt.size())
return true;
int i = bt[k].first;
int j = bt[k].second;
// fast path - only 1 possibility
if (cells[i][j].value)
return backtrack(k + 1);
auto constraints = cells[i][j].constraints;
// slow path >1 possibility.
// making snapshot of the state
array<array<cell,9>,9> snapshot(cells);
for (int v = 1; v <= 9; v++) {
if (!constraints[v]) {
if (set(i, j, v)) {
if (backtrack(k + 1))
return true;
}
// restoring from snapshot,
// note: computationally this is cheaper
// than alternative implementation with undoing the changes
cells = snapshot;
}
}
return false;
}
public:
void solveSudoku(vector<vector<char>> &board) {
cells = array<array<cell,9>,9>(); // clear array
// Decoding input board into the internal cell matrix.
// As we do it - constraints are propagated and even additional values are set as we go
// (in the case if it is possible to unambiguously deduce them).
for (int i = 0; i < 9; i++)
{
for (int j = 0; j < 9; j++) {
if (board[i][j] != '.' && !set(i, j, board[i][j] - '0'))
return; // sudoku is either incorrect or unsolvable
}
}
// if we're lucky we've already got a solution,
// however, if we have empty cells we need to use backtracking to fill them
if (!findValuesForEmptyCells())
return; // sudoku is unsolvable
// copying the solution back to the board
for (int i = 0; i < 9; i++)
{
for (int j = 0; j < 9; j++) {
if (cells[i][j].value)
board[i][j] = cells[i][j].value + '0';
}
}
}
};
作者说是2 ms,有人说跑的是 0 ms.
基本上这道题的核心是:空间换时间,1 ~ 9 暴力往上呼也不会差,从这个角度而言,没啥意思。
如果在此基础上能够缩小每个空格备选的范围,会省时间,
如果能再对可能性排序,那就算玩得有点儿意思了。