072 - Edit Distance

Edit Distance

Given two words word1 and word2, find the minimum number of steps required to convert word1 to word2. (each operation is counted as 1 step.)

You have the following 3 operations permitted on a word:

a) Insert a character
b) Delete a character
c) Replace a character

Hide Tags

Dynamic Programming String

Hide Similar Problems

(M) One Edit Distance

眼界不够，看了wiki 才知道这个问题还是有来头的。
先说题目本身，解完了再说它的渊源。

把两个字符串分别放在 DP 的矩阵横向/纵向的两个邻边，
如果在某个格子（x，y）从两个字符串里取到的字符不同， 则可能要进行三种操作：插入，删除，替换。
仔细观察可以知道，插入，删除，替换分别对应动态编程中的向右，向下，向右下：
    向下说明要在纵向的字符串里多跳过一个字符，然后再与横向字符串的下一个比较；
    向右则反之，说明要跳过横向字符串里的下一个字符，去跟下下一个字符比较；
        也就是说，实际上对一个字符串的删除，等效于对另一个字符串的插入。
    而向右下，则是直接把一个字符串中的字符替换成另一个中的字符。
    所以此时当前格子的值就是取这三个操作中最小的一个（就是要找最小的嘛），加上当前的操作cost（1）；
而如果取到字母相同，很显然无需额外操作，只需要继承之前的结果，也就是 （x-1，y-1）里面的值就可以了。

由此可以得到如下解答：
构建 DP 矩阵 mtx，两字符串居于邻边，但从 1 开始，而不是 0，因为主要的计算在矩阵中间。
注意首行/列分别对应其中一个字符串为空的情形，也就说，步步都插入，所以distance就等于下标：
                       
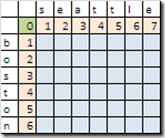
然后依照规则填写，（1,1）分别对应 b 和 s，所以是取 0 再加 1 = 1；（1,2）则是 1+1=2，（1,3）则是继承 2；……
最终将得到右侧的表格，最后一个格子的 6 就是需要的最小步骤了。

class Solution {
public:
    int minDistance(string word1, string word2) {
        int len1=word1.length()+1, len2=word2.length()+1;
       
        //use vector get 28 ms, use array get 16 ms.
        //vector<vector<int>> mtx(len1, vector<int>(len2, 0));
        int mtx[len1][len2];                    //will initialize later
        for(int x=0; x<len1; ++x)
        {
            mtx[x][0] = x;                      //initialization as if word2 is an empty string
            for(int y=1; y<len2; ++y)
            {
                if(word1[x-1]==word2[y-1])
                    mtx[x][y] = mtx[x-1][y-1];
                else
                    mtx[x][y] = (!x) ? y :      //initialization as if word1 is an empty string
                        //updating minimal distance needed of replace/insert/delete
                        (1 + min(mtx[x-1][y-1], min(mtx[x-1][y], mtx[x][y-1])));
            }
        }
        return mtx[len1-1][len2-1];
    }
};
16 ms.

这个问题的确是有来头的，而且在自然语言处理，拼写检测，生物识别等等领域都是相当重要的。（wiki）
这里的问题是简化过的，实际上还应该带上每个操作的权重，这样就更接近实际问题的处理了：
   
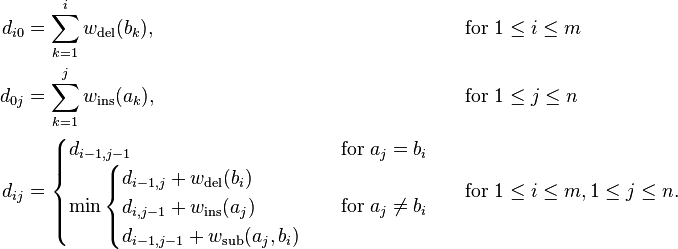
关于它的算法，DP 有两种，一种是如上面的用二维矩阵，空间是 O(mn)，另一种是用两个一维数组来滚动，空间是 O(m+n)，
另外还有一种改进的Hirschberg's algorithm，空间只是 O(min{n,m})。

另一个有意思的是，如果把三个操作中的替换去掉，只能增减的话，它就是 LCS (Longest common subsequence) 了；
而如果只是允许替换的话，（对于长度相等的字符串），它实际上就成了Hamming distance。

还有一些其他的演化，例如：
实际的字符串检测中还有一个常见的场景：两个相邻字符位置反了，因此还可以有一个操作，叫做互换（transposition），
另外在 OCR 输出校对的时候，还有 merge 和 split 操作，做一对多的更为复杂的替换。